A simple pendulum hangs from the roof of a train moving on horizontal rails. If the string is inclined towards the front of the train, then train is-

1. Moving with constant velocity

2. In accelerated motion

3. In retarded motion

4. At rest

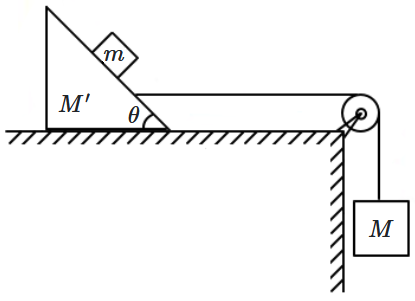
The value of \(M\) of the hanging block is in the figure, which will prevent the smaller block (\(m\)\(=\)\(1\) kg) from slipping over the triangular block. All the surfaces are smooth and string and pulley are ideal. (Given: \(M'\)\(=4\) kg and \(\theta\) \(=37^\circ\))

           
1. \(12\) kg
2. \(15\) kg
3. \(10\) kg
4. \(4\) kg

A lighter body and heavier body both are moving with same momentum and applied same retarding force. Their stoping distances are $s_1<mspace\; width="1em"></mspace>and<mspace\; width="1em"></mspace>s_2$ respectively. Then the correct relation between $s_1<mspace\; width="1em"></mspace>and<mspace\; width="1em"></mspace>s_2$-

1. $s_1>s_2$

2. $s_1<s_2$

3. $s_1=s_2$

4. None of these

A simple pendulum (bob of mass \(m\)) oscillates in a vertical plane. Let \(\theta\) be the angular displacement from the vertical. The tension in the string is equal to \(mg \mathrm{cos\theta}\) under which condition?
1. Always
2. never
3. At the extreme position
4. At the mean position

The graph for stopping time \((t)\) versus mass \((m)\) is shown in the figure. Then which one of the pairs is given?

1. Momentum, force

2. K.E., force

3. Velocity, force

4. None of these

While walking on ice one should take small steps to avoid slipping. This is because smaller steps ensure

1. Larger friction

2. Smaller friction

3. Larger normal force

4. Smaller normal force

A block is placed on a rough horizontal plane. A time dependent horizontal force F=kt acts on the block. The acceleration time graph of the block is :

1.		2.
3.		4.

A motorcycle is going on an overbridge of radius R. The driver maintains a constant speed. As the motorcycle is ascending on the overbridge, the normal force on it:

1.  Increases

2.  decreases

3.  remains the same

4.  fluctuates erratically

Two blocks A and B of masses m & 2m respectively are held at rest such that the spring is in natural length. Find the accelerations of both the blocks just after release.

1. \(g \downarrow ,   g \downarrow\)

2. \(\frac{g}{3} \downarrow ,   \frac{g}{3} \uparrow\)

3. (0, 0)

4. \(g \downarrow ,   0\)