An electron moves on a straight-line path \(XY\) as shown. The \(abcd\) is a coil adjacent to the path of the electron. What will be the direction of the current, if any induced in the coil?
             

1.	\(abcd\)
2.	\(adcb\)
3.	The current will reverse its direction as the electron goes past the coil.
4.	No current is induced.

A wire loop is rotated in a magnetic field. The frequency of change of direction of the induced emf is

(1) once per revolution

(2) twice per revolution

(3) four times per revolution

(4) six times per revolution

A coil of resistance 400$\Omega$ is placed in a magnetic field. If the magnetic flux $\varphi \left(Wb\right)$ linked with the coil varies with time t (sec) as $\varphi =50t^2+4.$

The current in the coil at t=2s is 

(1) 0.5A                                           

(2) 0.1A

(3) 2A                                               

(4) 1A

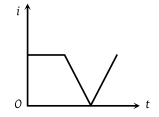
The current i in an induction coil varies with time t according to the graph shown in figure. Which of the following graphs shows the induced emf (e) in the coil with time

1.              2.
3.               4. 

A flexible wire bent in the form of a circle is placed in a uniform magnetic field perpendicular to the plane of the coil. The radius of the coil changes as shown in the figure. The graph of induced emf in the coil is represented by

1.

2.

3.

4.

A rectangular loop is being pulled at a constant speed v, through a region of certain thickness d, in which a uniform magnetic field B is set up. The graph between position x of the right-hand edge of the loop and the induced emf E will be-

1.  2. 

3.  3. 

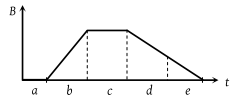
The graph gives the magnitude B(t) of a uniform magnetic field that exists throughout a conducting loop, perpendicular to the plane of the loop. Rank the five regions of the graph according to the magnitude of the emf induced in the loop, greatest first

1. b > (d = e) < (a = c)

2.  b > (d = e) > (a = c)

3. b < d < e < c < a

4. b > (a = c) > (d = e)

A conducting rod AC of length 4l is rotated about a point O in a uniform magnetic field $\overrightarrow{B}$ directed into the paper. AO = l and OC = 3l. Then

1. $V_A-V_O=\frac{B\omega l^2}{2}$

2. $V_O-V_C=\frac{7}{2}B\omega l^2$

3. $V_A-V_C=4B\omega l^2$

4. $V_C-V_O=\frac{9}{2}B\omega l^2$

A wire cd of length l and mass m is sliding without friction on conducting rails ax and by as shown. The vertical rails are connected to each other with a resistance R between a and b. A uniform magnetic field B is applied perpendicular to the plane abcd such that cd moves with a constant velocity of

1. $\frac{mgR}{Bl}$

2. $\frac{mgR}{B^2{l}^2}$

3. $\frac{mgR}{B^3{l}^3}$

4. $\frac{mgR}{B^{2}l}$

A rectangular loop with a sliding connector of length \(l= 1.0\) m is situated in a uniform magnetic field \(B = 2T\) perpendicular to the plane of the loop. Resistance of connector is \(r=2~\Omega\). Two resistances of \(6~\Omega\) and \(3~\Omega\) are connected as shown in the figure. The external force required to keep the connector moving with a constant velocity \(v = 2\) m/s is:

          
1. \(6~\text{N}\)
2. \(4~\text{N}\)
3. \(2~\text{N}\)
4. \(1~\text{N}\)