A simple pendulum hanging from the ceiling of a stationary lift has a time period T1. When the lift moves downward with constant velocity, the time period is T2, then
(a) is infinity
(b)
(c)
(d)
एक स्थिर लिफ्ट की छत से लटकने वाले एक सरल लोलक का दोलन काल T1 है। जब लिफ्ट नियत वेग से नीचे की ओर गति करती है, दोलन काल T2 है, तब
(a) अनंत है
(b)
(c)
(d)
One end of a long metallic wire of length L is tied to the ceiling. The other end is tied to massless spring of spring constant K. A mass m hangs freely from the free end of the spring. The area of cross-section and Young's modulus of the wire is A and Y respectively. If the mass is slightly pulled down and released, it will oscillate with a time period T equal to -
(a) (b)
(c) (d)
L लंबाई के एक लंबे धातु के तार का एक सिरा छत से बांधा गया है। दूसरा सिरा स्प्रिंग नियतांक K की द्रव्यमानरहित स्प्रिंग से बांधा गया है। एक द्रव्यमान m स्प्रिंग के मुक्त सिरे से स्वतंत्र रूप से लटका हुआ है। तार के अनुप्रस्थ-काट का क्षेत्रफल और यंग का मापांक क्रमशः A और Y है। यदि द्रव्यमान थोड़ा नीचे खींचा और छोड़ा जाता है, तो यह आवर्तकाल T से दोलन करेगा, जो बराबर है -
(a) (b)
(c) (d)
One end of a spring of force constant k is fixed to a vertical wall and the other to a block of mass m resting on a smooth horizontal surface. There is another wall at a distance from the block. The spring is then compressed by and then released. The time taken to strike the wall is :
1.
2.
3.
4.
k बल नियतांक की स्प्रिंग के एक सिरे को ऊर्ध्वाधर दीवार से और दूसरे को चिकनी क्षैतिज सतह पर विरामावस्था पर स्थित द्रव्यमान m के गुटके से जोड़ दिया जाता है। गुटके से दूरी पर एक और दीवार है। तब स्प्रिंग को से संपीडित किया जाता है और फिर मुक्त कर दिया जाता है। दीवार से टकराने में लगे समय की गणना कीजिए:
1.
2.
3.
4.
A piece of wood had dimensions a, b and c. Its relative density is d. It is floating in water such that the side c is vertical. It is now pushed down gently and released. The time period is:
1.
2.
3.
4.
लकड़ी के एक टुकड़े की विमाएँ a, b और c है। इसका सापेक्षिक घनत्व d है। यह जल में इस प्रकार तैर रहा है कि भुजा c ऊर्ध्वाधर है। अब इसे धीरे से नीचे धकेला जाता है और मुक्त किया जाता है। आवर्तकाल की गणना कीजिए:
1.
2.
3.
4.
The equation of a simple harmonic oscillator is given as , where t is in seconds. The frequency with which kinetic energy oscillates is
1. 5 Hz
2. 10 Hz
3. 20 Hz
4. 40 Hz
किसी सरल आवर्ती दोलन के समीकरण को द्वारा व्यक्त किया गया है, जहां t सेकेंड में है। वह आवृत्ति ज्ञात कीजिए जिसके साथ गतिज ऊर्जा दोलन करती है?
1. 5 Hz
2. 10 Hz
3. 20 Hz
4. 40 Hz
If a simple pendulum is brought deep inside a mine from earth surface, its time period of oscillation will
1. Increase
2. Decrease
3. Remain the same
4. Any of the above depending on the length of the pendulum
यदि एक सरल लोलक को पृथ्वी की सतह से एक खदान के अंदर गहराई में ले जाया जाता है, तब इसके दोलन का आवर्तकाल किस प्रकार प्रभावित होगा?
1. बढ़ेगा
2. घटेगा
3. समान रहेगा
4. लोलक की लंबाई के आधार पर उपरोक्त में से कोई भी
A particle executes S.H.M with amplitude A. If the time taken by the particle to travel from -A to A/2 is 4 seconds, its time period is
1. 4s
2. 8s
3. 12 s
4. 18 s
एक कण आयाम A के साथ सरल आवर्त गति करता है। यदि कण को A से A / 2 तक जाने में लगने वाला समय 4 सेकेंड है, इसका आवर्तकाल ज्ञात कीजिए:
1. 4s
2. 8s
3. 12 s
4. 18 s
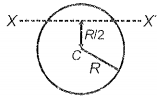
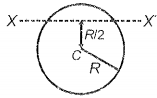
A disc executes S.H.M. about the axis XX' in the plane of the disc as shown in the figure. Its time period of oscillation is:
1.
2.
3.
4.
एक डिस्क आरेख में दर्शाए गए अनुसार, डिस्क के तल में XX' अक्ष के परितः सरल आवर्त गति करती है। इसके दोलन के आवर्तकाल की गणना कीजिए:
1.
2.
3.
4.
The potential energy of a particle of mass m executing SHM is given by U = A(1 - cos2x), where x is the instantaneous displacement of the particle. The time period of oscillation is
1.
2.
3.
4.
सरल आवर्त गति का निष्पादन कर रहे m द्रव्यमान के एक कण की स्थितिज ऊर्जा U = A (1 - cos2x) द्वारा दी गयी है, जहां x कण का तात्कालिक विस्थापन है। दोलन का आवर्तकाल है
1.
2.
3.
4.
A simple pendulum with a metallic bob has a time period T. The bob is now immersed in a nonviscous liquid and the time period is found to be T. The ratio of the density of the metal to that of liquid is
1. 1/4
2. 4/3
3. 5/4
4. 7/3
धात्विक गोलक के साथ एक सरल लोलक का आवर्तकाल T है। अब गोलक एक अश्यान द्रव में डुबोया जाता है और आवर्तकाल T पाया जाता है। धातु के घनत्व का द्रव के घनत्व से अनुपात है:
1. 1/4
2. 4/3
3. 5/4
4. 7/3







